結び目の数学 †
結び目とは結ばれている一本の紐です.靴の紐やお祝い事の水引を想像してみて下さい.
驚くことに日常の中に溢れているその結び目が数学の研究対象となっています.
結び目理論の研究は
「与えられた2つの結び目が同じかどうかを判定せよ」
という問題を考えることが基本です.
ここでは,紐を切らずに連続的に動かして同じ形になる結び目たちを同じとみなします.
これはトポロジーという数学の一分野の考え方です.
 |
|
 |
|
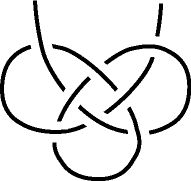 |
| (a) 結ばれてない紐 |
|
(b) 片結び |
|
(c)
あわび結び |
一見すると図1(a)は結ばれていない紐で(b)や(c)は結ばれています.
しかし(b)や(c)の紐は端をスルスルっと動かすと紐を切らずに(a)の状態になるので
結ばれていないものと同じになります.つまり端があるとすべて結ばれていないのです.
これではツマラナイ.
![[sad]](sad.png)
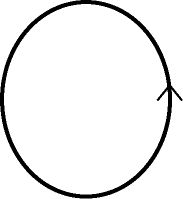
よって数学として結び目を考えるときは結ばれた両端のある一本の紐ではなく
図2のように,その端をくっつけて閉じた輪として見ます.
数学的にかしこまっていうと,結び目とは
3次元ユークリッド空間に埋め込まれた1つの円周のことです.
 |
|
 |
|
 |
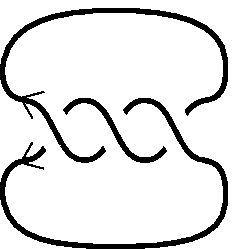
| (a) 自明な結び目 |
|
(b) 三葉結び目 |
|
(c)
あわび結び目 |
結び目が同じかどうかを判定するのが基本問題と書きましたが,
どうやって判定するのでしょう.グニャグニャと変形させて同じ形になれば
同じなのですが、違うことを判定する,
数学的にいうと違うことを証明するのは厄介だと気づかれるでしょう.
1000回グニャグニャと変形させて同じにならないとしても,それはやり方が悪いだけで
1001回目には上手くいくかもしれません.何回やっても駄目だから「違う」とは
いえないのです.
つまり直感では図2(b)の三葉結び目が解けていないことは分かっていても,
それだけでは数学的には解けていないことが分かった!とは言わないのです.
(図3の結び目は複雑ですが、結ばれてますか?)
この「違うことを証明する」ために,結び目理論では主に不変量というものが研究されていました.結び目の不変量とは数値や数式など,結び目に対して定義されたある数学的な量のことで,
同じ結び目なら同じ量となる
もののことをいいます.例えば,Alexander多項式という不滅の不変量があります.
これは1変数の多項式で,図2のような結び目の図式から計算されるものですが,
同じ結び目を表しているようなどんな図式から計算しても同じ式になるように定義されています.
(これが不変量であるということ.)
解けている自明な結び目では 1 という式になりますが,
三葉結び目では 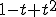 という式になります.こうして,
という式になります.こうして,
不変量というものを見比べてみて初めて, 三葉結び目が自明な結び目と同じではない,
つまりほどけていないことが分かるのです.
しかしこのAlexander多項式も完全ではありません.Alexander多項式が1であるが,
解けていない結び目がたくさん存在します.(これには他の方法で違いを判定します.)
ここが結び目理論の難しく,面白いところです.
私の研究
このように結び目理論では分類問題の解決のため様々な不変量が開発されてきました.
現在,私は上述した(詳しく説明していないが)Alexander多項式のような
代数的な不変量と結び目の幾何的な性質の関連を研究しています.
分類が直接の目的ではないこのような研究も,結び目理論の中心課題なのです.
特に結び目の図式(ダイアグラム)を視点とした研究をしています。
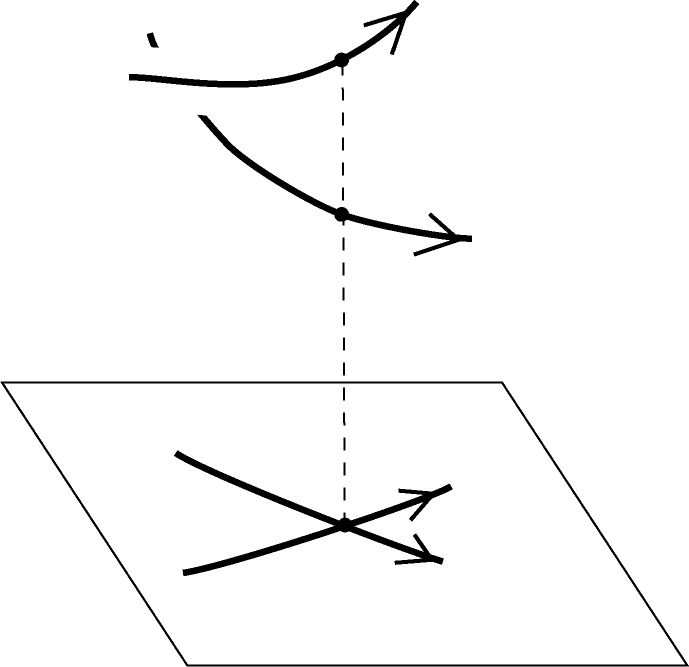
空間内の向きの付いた結び目を平面上に2重点のみを持つように射影し,
各交差に射影前の上下の情報を加えた図をダイアグラムといいます.(図4(a)参照。)
向きの付いた結び目のダイアグラムの各交点には一般に正(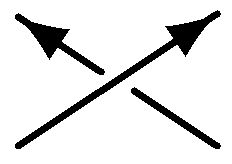 )と負( )と負(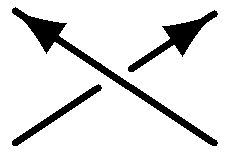 )の2種類が現れます. )の2種類が現れます.
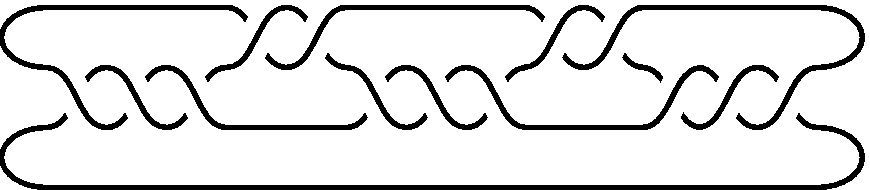
空間内のある方向に関して2個の極大点を持つ2橋結び目(図4(b))や
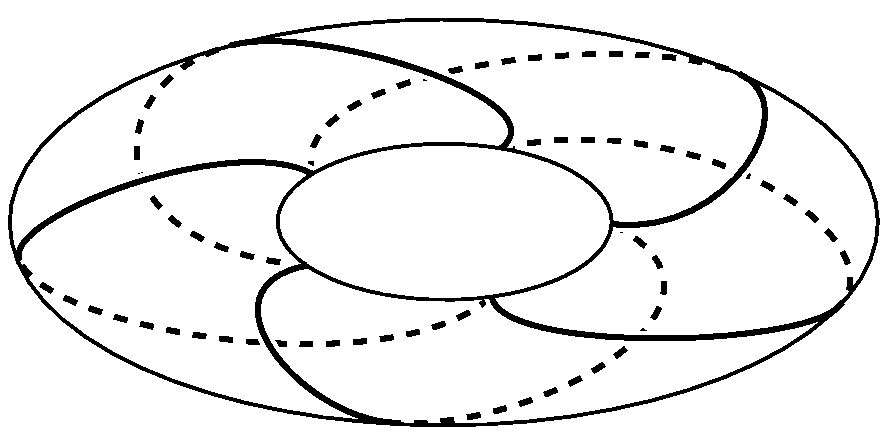
標準的なトーラス(輪環面)の上に交差を作らずに描けるトーラス結び目(図4(c))など
多くの結び目がそのトポロジカルな性質で定義されその性質を端的に表す
ダイアグラムを持ちます.つまり結び目の幾何がダイアグラムに現れています.
 |
 |
 |
| (a) 結び目の射影 |
(b) 2橋結び目 |
(c)
トーラス結び目 |
逆に交代結び目のようにダイアグラムの性質で定義された結び目も多くあります.
ダイアグラムを辿って一周したとき交差の上下が交互に現れる図式を
交代ダイアグラムといい,それを持つ結び目を交代結び目といいます.
(図2の三葉結び目やあわび結び目など。)
交代結び目は古くから研究されAlexander多項式の特徴,
種数や最小交点数と
いった幾何的量など多くの性質が分かっています.しかし,この交代的という
ダイアグラムの性質は大域的なもので,結び目本来の性質といえます.そこで
ダイアグラム自体が持つ性質に着目し,それが与える結び目の複雑さを解明する
ことをテーマとし,研究を進めてきました.
特にすべての交点が正である正ダイアグラムを持つ正結び目の幾何的,代数的性質の研究,及び,ダイアグラムから得られる標準的曲面の研究がメインテーマで今後もその研究を進めていきます.
主な研究業績
- Takuji NAKAMURA, Four-genus and unknotting number of positive knots and
links, Osaka J. Math., Vol. 37, No. 2, 441-451 (2000).
- Takuji NAKAMURA, Notes on the barid index of closed positive
braids, Topology and its Applications, Vol. 135, No.1--3, 13-31 (2004).
- Takuji NAKAMURA, Notes on braidzel surfaces for links, Proc. Amer.
Math. Soc. より掲載受理.
|