大学院 工学研究科 先端理工学コース 准教授
筑波大学
学生時代には自転車での日本縦断経験あり。その時から使い込んでいる愛車・ランドナーで週末は淀川沿いを走っています。また3歳頃からピアノにも親しんでおり、特にショパン・リスト・ラフマニノフなどロマン派の作曲家がお気に入りで、休日に練習しています。
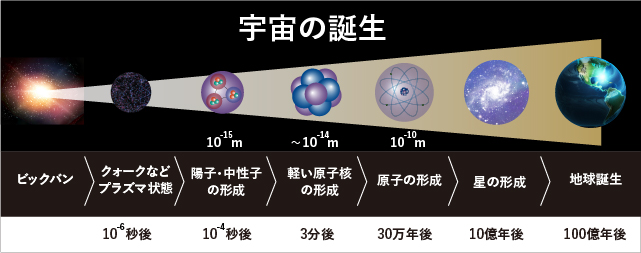
18世紀から22世紀へ
数学のバトンを受け渡す「概均質ベクトル空間」に挑む
数学上の発見は、ある日突然なされるものではありません。ある数学者が取り組んだ問題を、次の世代の数学者が受け継いで新たな理論を生み出し、そのまた次の世代の数学者がその理論に別の角度から光を当てることで、少しずつ洗練されていきます。
名倉准教授も、まさにそんな数学者のひとりです。何百年に渡る数学史の流れの中で「概均質ベクトル空間」の分類と数え上げという壮大なテーマに取り組んでいます。
日本で生まれた「概均質ベクトル空間」
その種類を分類し、数え上げる研究に取り組む
時は18世紀。数学オイラーは、円周率πを使えば ゼータ関数の値を非常にシンプルに記述できると気づきました。その後19世紀になると、ゼータ関数は数学者リーマンによって、さらに虚数iも含む全複平面上に拡張され、次の関数等式を満たすことがわかってきました。
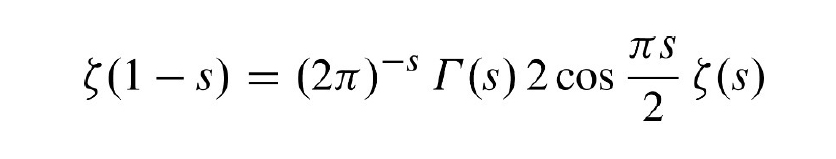
20世紀になり、このリーマンのゼータ関数等式が成り立つ理由をはっきりと筋道立てて説明する理論のひとつが誕生します。その理論はなんと日本生まれ。佐藤幹夫博士によって創始された「概均質ベクトル空間」です。佐藤博士と木村達雄博士は、この概均質ベクトル空間のうち、ある種類のものが29種類あると突き止めましたが、そこには「複素数体C上の既約正則な」という仮定がついていました。
では、こうした仮定を取り除いたときに、概均質ベクトル空間は何種類存在するのでしょうか。
21世紀の現在、木村博士の下で学んだ名倉准教授は、その種類を分類し数え上げる研究に取り組んでいます。たくさんある空間のうち、どれが同じで、どれが異なるのかを区別して分類することは、「数学の実験」をするための「(異なる)場所を提供する」という意味で、とても重要な意味を持ちます。
ディンキン型クイバーに付随する概均質ベクトル空間を
「ルート系」「カタラン数」を使って分類し、数え上げる
名倉准教授が特に注目しているのが、有向グラフ「クイバー」に付随する概均質ベクトル空間です。
なかでもディンキン型クイバーは、数学のさまざまな分野に現れる基本的なグラフです.このディンキン型クイバーに付随する概均質ベクトル空間は、「ルート系」と呼ばれるベクトルの配置を使うと、急に分類の見通しが良くなり、数え上げられるようになります。またディンキン型クイバーに付随する「正則」と呼ばれる概均質ベクトル空間の個数も、カタラン数を使うと数えることができるようになります。
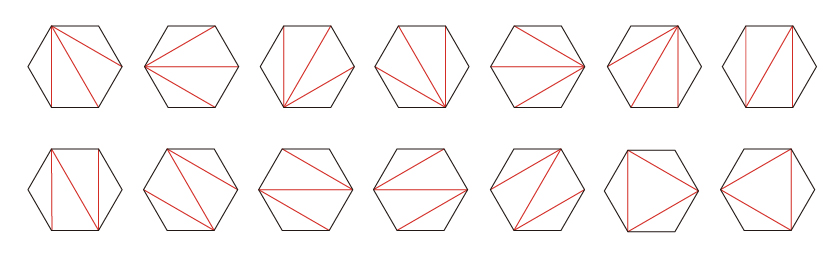
6角形を三角形に分割する方法の場合はC4=14で,上の図のように14通りある.
このほか概均質ベクトル空間全体を図示すると、きれいな多面体が現れることがあります。一見複雑に見えることも、ある数学的な見方をするとシンプルに見通せるようになります。これが数学の面白さです。
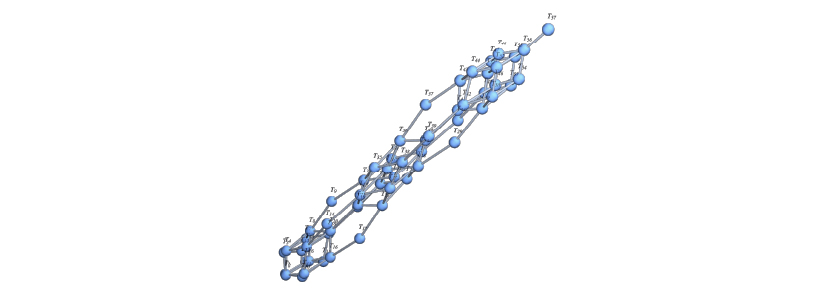
名倉研究室のテーマは、整数論、代数や数え上げ数学など、数の種類を分類して数え上げる純粋数学です。
純粋数学は社会に直接的に役立つわけではありませんが、目の前の何かを数えることは、人間が持つ大きな欲求のひとつです。名倉研究室には教職志望者も多く、数の秘密を解くことが人生でどう役に立つのかを、常に意識しながら研究に取り組める環境があります。この研究室から22世紀へとバトンを繋ぎ、未来の子どもを育てる晴らしい数学の教員が、数多く誕生することを期待します。
見えなかったものが、見えてくる
数学は新しい物の見方を生むツール
「素数が無限個ある」ことはゼータ関数で証明できます。また、名倉准教授の研究では、概均質ベクトル空間全体の中に多面体が現れることがわかってきました。数学を使うと、見えないものが見え、解けなかった問題がよりシンプルに解けるようになります。純粋数学とは、実は社会に生きるひとに役立つ「新しい物の見方」「新しい視点」を提供する学問でもあるのです。
各種取材や研究に関することなど、
お気軽にお問い合わせください