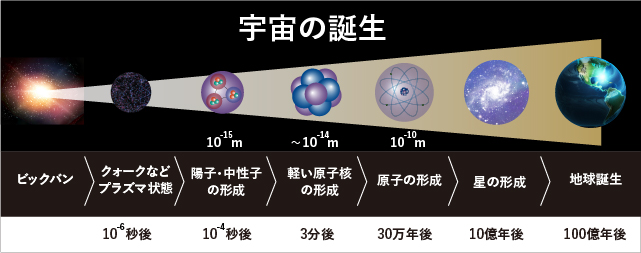
神戸大学
運動不足解消に大学院時代からフットサルを始めました。今もワイワイ楽しみながら練習・試合ができるスクールに週1ペースで通っています。兵庫県出身なので、サッカーは地元ヴィッセル神戸を応援。
また紫垣家のルーツは九州のため、ラーメンは断然とんこつ派です。教育と研究を両立させながら、忙しくも充実した日々を過ごしています。
常微分方程式の固有値問題に
完全WKB解析を用いてアプローチ
数学における重要な分野である微分方程式には、多彩な研究テーマが存在します。
紫垣特任講師は、その中のひとつ「常微分方程式の固有値問題」に挑戦しています。なかでも、完全WKB解析の手法を用いて、様々な固有値問題を扱うことを模索しています。
完全WKB解析とBorel総和法
微分方程式の微小なパラメータに関する級数解(WKB解)を考え、これを最初の数項で打ち切って近似する手法が、物理学では「WKB近似」と呼ばれています。

シュレーディンガー方程式と呼ばれる微分方程式の解を近似し, 物理的に有用な情報を引き出したのがWKB近似である.
一般には級数の項をたくさん足すほど「良い近似」になると期待されるので、すべての項を「完全に」考えればもっとよく分かるはずだという理念に基づき発展したのが「完全WKB解析」です。
ただし、無限個の項を足したもの(無限級数)は、必ずしも数学的に意味を持つとは限りません。たとえば、「1+1/2+1/4+1/8+ ⋯」と足し合わせていくと、どんどん2に近づきます。このように無限に足し合わせて特定の値に近づくことを「収束」と呼びます。
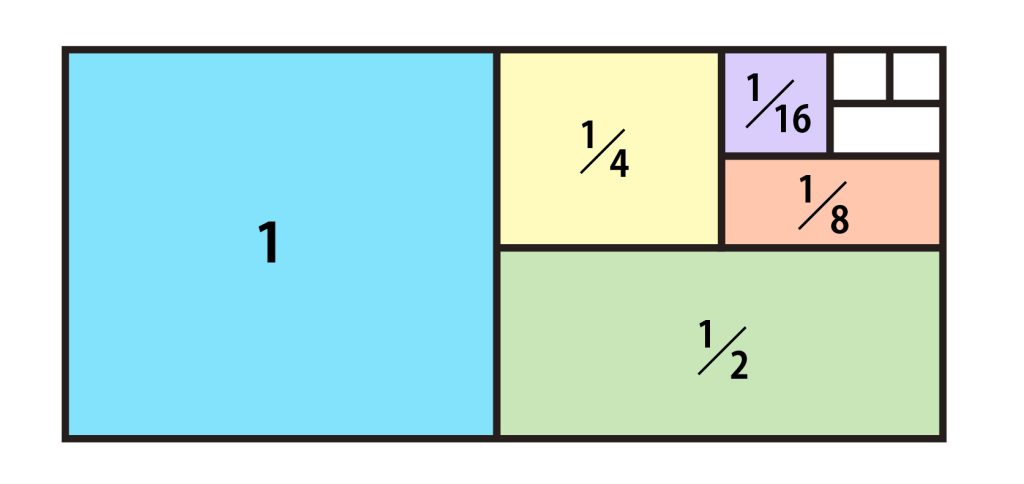
水色の面積を1とすると, 緑色の面積が1/2, 黄色の面積がその半分で1/4, 桃色が1/8, 紫色が1/16,… となり, 和はどんどん2に近づくことが視覚的に分かる.
一方で、「1+2+3+4+⋯」と足し合わせていく場合は、特定の値に近づくことはなく、無限に大きくなります。このことを「発散」と呼びます。この「発散する級数」に対して、ある種の数学的に意味がある値を与えるための操作を総和法といいます。
完全WKB解析においては、総和法の一種である Borel総和法を用いてWKB解に数学的な意味を与える、という工夫を行います。
紫垣特任講師は、いくつかの具体的な固有値問題に対し、WKB解に数学的意味を与えること(Borel総和法を用いることができることの証明)や、WKB解の接続公式を用いた固有値の条件式(の主要部)を導き出しました。
完全WKB解析が
具体的ないくつかの固有値問題に応用できる可能性を広げる
ある方程式の変数がたとえば無限大に近づいた場合「解の値がどのくらい大きくなるか・小さくなるか」という条件によって興味のある解の条件を定めると、一般的には条件を満たす解が存在するケースと存在しないケースがあります。
条件を満たす解が存在する場合、定めた条件から特定のパラメータが決まり、そのパラメータの値を固有値と呼びます。完全WKB解析では解の解析接続の様子がよく分かるため、特に無限大に近づいたときの解の変化の仕方も得られ、固有値問題を考える上で非常に有用と言えるでしょう。
固有値問題は数学の由緒正しき問題のひとつで、物理との関係も深い問題のひとつです。紫垣特任講師は、2つのテーマの固有値問題に対し、完全WKB解析によるアプローチとして一定の成果を得ました。これらのテーマについてさらに研究を進めながら、似た手法が他の固有値問題にも応用できないか?と模索しています。
固有値問題と密接にかかわる
物理分野への応用が期待される!
紫垣特任講師の取り組んでいる「固有値問題」は数学の由緒正しき問題のひとつです。この「固有値問題」は、物理学とも密接にかかわっています。
完全WKB解析が「固有値問題」の研究に有用であることが、広く知られるようになれば、紫垣特任講師の夢でもある“完全WKB解析の分野への恩返し”になるだけでなく、物理学をはじめ関連分野との連携や応用なども期待できます。
各種取材や研究に関することなど、
お気軽にお問い合わせください