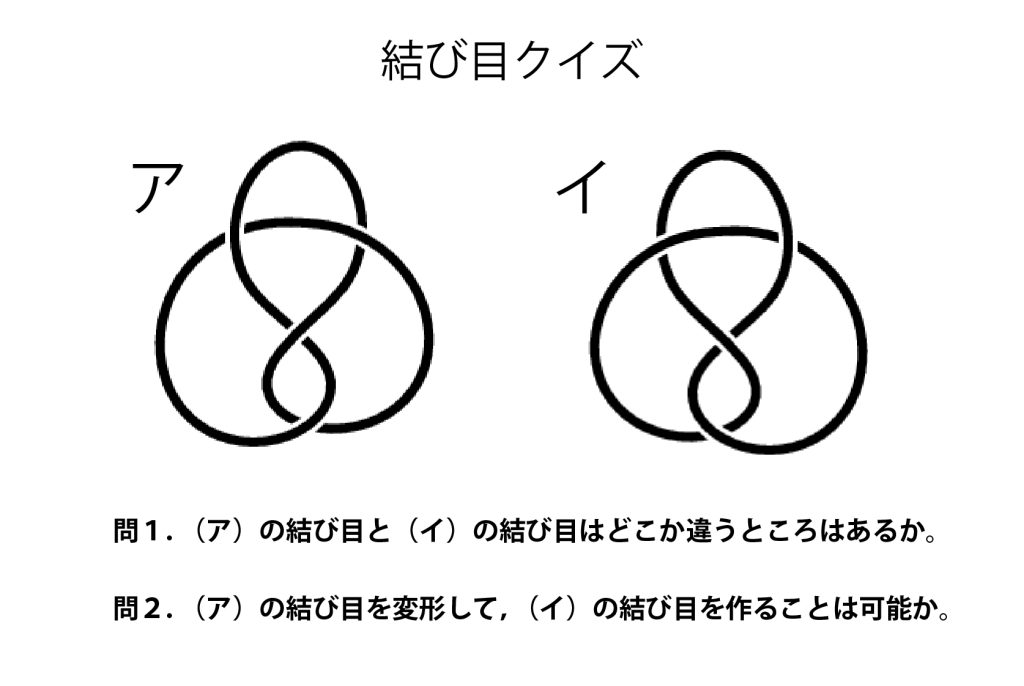
多重ゼータ値に関する関係式を探究し　
世紀の難問「ザギエ予想」に挑む！

数学には「○○予想」と呼ばれるものがあります。ある数学者が「まだ証明はできていないけれど、きっとこうなるはずだ」と立てた仮説のことで、「リーマン予想」や「P≠NP予想」がその代表です。数学には、こうした未解決問題が数多く存在しています。
若林准教授は、そんな未解決問題のひとつである「ザギエ予想」について、２つのアプローチから取り組んでいます。

数を限りなく足していくとどうなる？　
無限和に秘められた謎に挑む数学者たち

自然数の無限和（限りなく足し合わせた結果）は無限大になります。では、自然数の逆数の無限和は？ これも無限大になります。

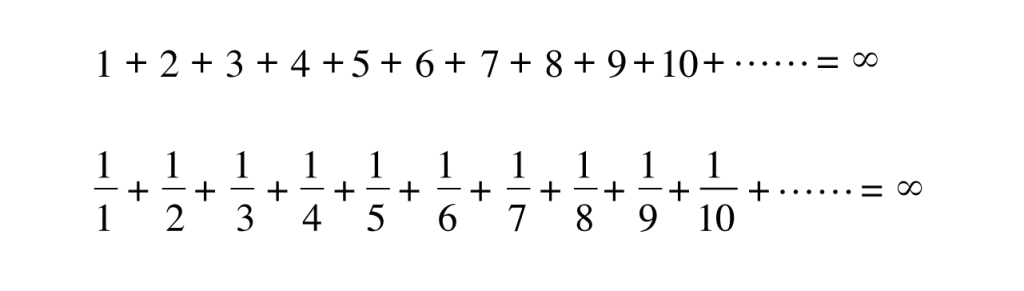
さらに、自然数の逆数のべき乗の無限和はどうなるでしょうか。

これも無限大になるかというと、そうではありません。逆数のべき乗の場合、その無限和は無限ではない数に収束します。そして、数学者オイラーは1735年、この無限和を円周率πを使って非常にシンプルに記述できることを発見しました。

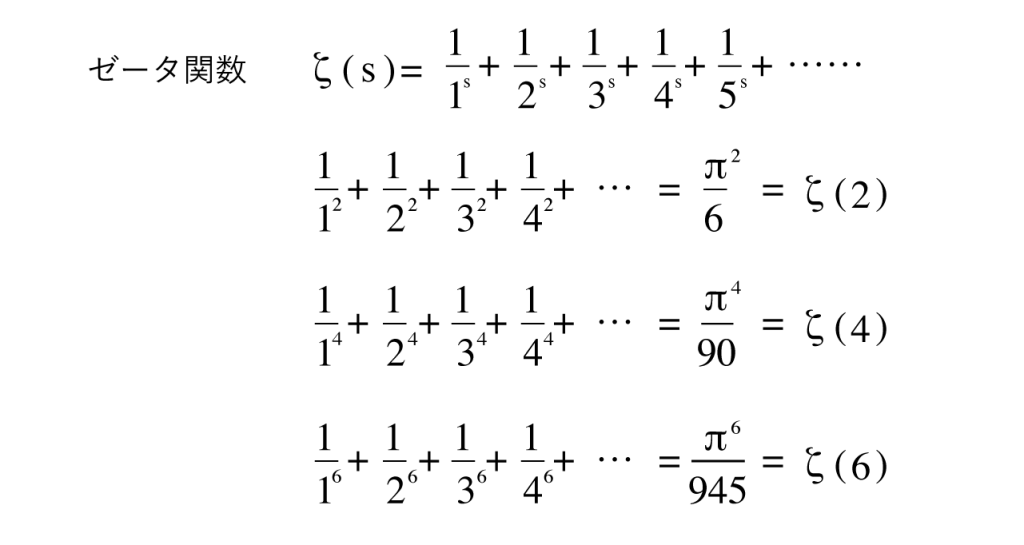
300年近くも前に、手計算で上記の美しい「オイラーの公式」が導き出されたのは驚くべきことですが、解明されたのは式を見てわかる通り偶数乗の時のみでした。

その後、数学者リーマンが、このオイラーの公式をゼータ関数として考案し、さらに無理数を含む実数に広げ、リーマンゼータ関数として下記のように記述します。

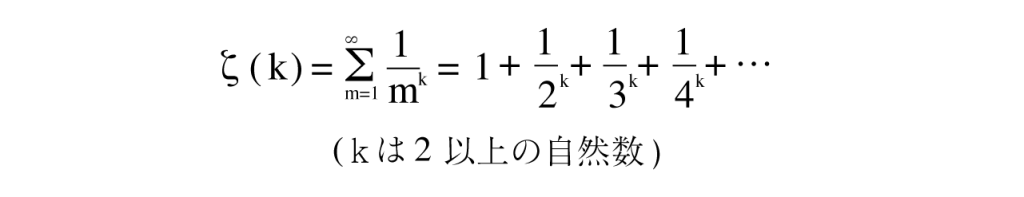
そして、このリーマンゼータ関数を、一般化したものを多重ゼータ値と呼び、以下の関数で表します。

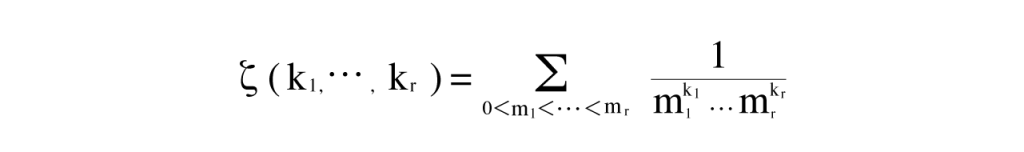
多重ゼータ値の中に必ず鍵が眠っている　
２つの方向から関係式の発見に迫る

若林准教授は、この「多重ゼータ値」を研究しています。多重ゼータ値には、さまざまな関係式が成り立つと予想されており、最も有名なのは1990年代には数学者ザギエが提唱した次元予想です。

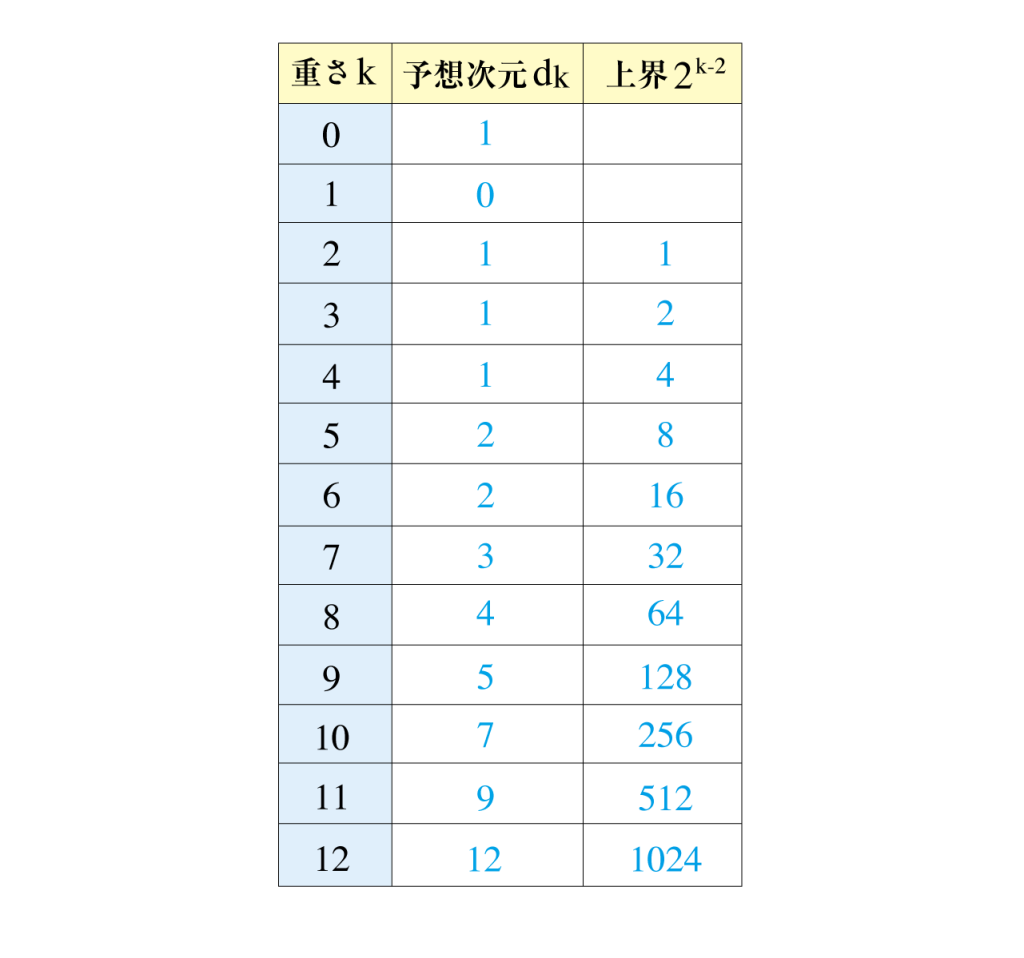
ザギエ予想はリーマン予想よりも難問ともいわれています。簡単にいうと、たとえば上記で重さ12の許容インデックスは1024個ですが、本質的に意味のあるものは12しかないはずだという予想です。その意味のあるものをあぶり出すための関係式の発見に向けて、日々研究を続けているのです。

また同時に、若林准教授は多重ゼータ値に対し、異なる面からのアプローチも行っています。それが、根付き木写像と呼ばれるグラフを使った方法です。コンヌ‐クライマーによる根付き木のホップ代数が、多重L値の関係式に関わっている可能性について調べているのです。

現在もなお、奇数点におけるリーマンゼータ値にはまだ未解明な部分が数多くあります。しかし、多重ゼータ値や多重L値から新たな関係式が発見されれば、この問題についても、いずれ解ける日が来ると予想されます。