大学院 総合情報学研究科 コンピュータサイエンスコース 教授
新潟大学
休日にはよく料理をします。当初はレシピを見ながらでしたが、最近は目分量で好みの味に仕上げられるようになってきました。手順は単純なのに素材の味が生かせる中華料理がお気に入りです。
膨大な組み合わせが存在して正解が導けない
難解な「組み合わせ最適化問題」を解くには
どの道をどう通れば最も速く目的地に着けるか。カーナビのルート検索は、多くの組み合わせから最適なものを求める「組み合わせ最適化問題」の一つ。現実問題を数理モデルとして定式化し、計算によって答を導きます。
渡邊研究室では、「組み合わせ最適化問題」の基礎理論を研究しています。
アリがエサを運ぶ最短ルートを見つけ出す
生態をシミュレーションしたアルゴリズム
現実に起こる問題の多くが、「組み合わせ最適化問題」として定式化できます。トラックの台数が最小限ですむ配送ルート、コストを抑え収益を最大にする製造計画、過不足のないアルバイトの人員配置など経営上の問題にも応用されています。
渡邊研究室では、組み合わせが膨大にあって最適解を導くのが難しい問題を解く方法として、ある程度正解に近い解が導ける手法の改善を繰り返すメタヒューリスティック的と呼ばれる解法を研究。
たとえば、アリがエサを巣まで運ぶ最短経路を効率よく見つけ出す行動をシミュレーションした「アントシステム」。これを、テーマパークで最小限の待ち時間でアトラクションを回るアルゴリズムに応用するなど、さまざまな試みを行っています。
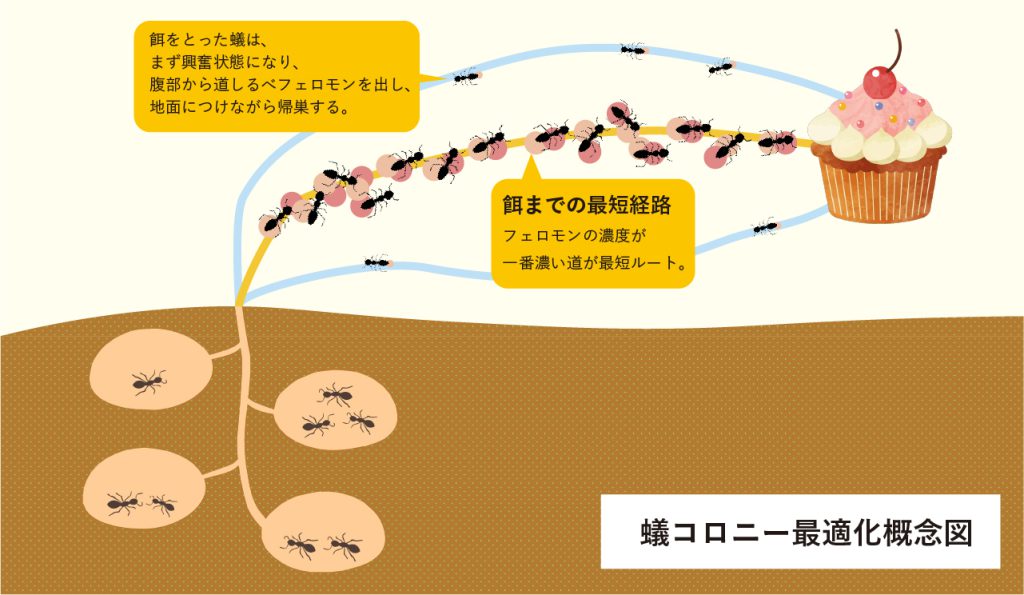
餌を見つけたアリは,腹部から道しるべフェロモンを地面につけながら巣に帰る.仲間のアリはフェロモンをたどって餌に向かう.餌からの距離が近ければフェロモンは濃く,遠回りであれば薄くなることから,自然に最短ルートが選別されていく.
現実の問題をグラフとしてモデル化し
条件に合った最適な解を見つける
またグラフ理論やネットワーク理論を使った「組み合わせ最適化問題」も研究テーマの一つ。「組み合わせ最適化問題」には、頂点を枝で結ぶグラフに数値データを付加する「ネットワーク理論」を応用するものが数多くあります。
たとえば、基本的な「ネットワーク理論」の一つである最大流問題は、始点から終点まで最大量を流す組み合わせを求める方法ですが、水や交通、電気や通信などの流れを扱うさまざまなシステムの構築や解析に広く応用できます。
また、頂点や枝を塗り分ける彩色問題の理論を使って、無線通信においてチャネルを効率的に割り当てる方法を導くことも。現実の問題をグラフやネットワークに抽象化して数式化することで、コンピュータで解ける問題にしていくものです。
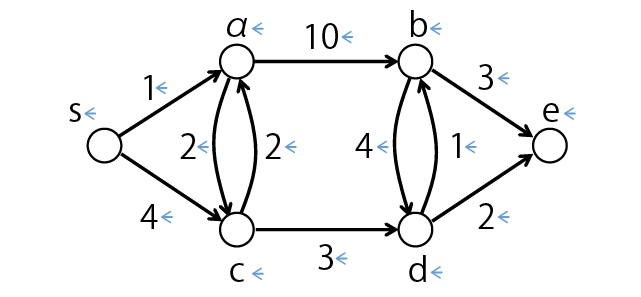
頂点を丸,頂点間の経路を矢印,頂点間の長さを数字で表し,最短経路を求める.この図のsからeへの最短経路は「s→a→c→d→e」.このような最短経路問題の考え方は,カーナビなどの探索に応用されている.
世の中を変えるような解法が見つかるか!?
常に進化を続ける最適化、アルゴリズム研究
社会のあらゆる場面で最適化問題が検討され、アルゴリズムが開発されています。しかし、最適解を見つけるのは簡単ではありません。厳密に最適解を求めるのは不可能、もしくは時間がかかりすぎる問題では、「だいたい正しい」解が得られればよしとしているのです。
社会をさらによくしたり、コンピュータの性能を向上させたりすることができる最適化やアルゴリズムは、常に進化途上の技術。次に生まれる新たな解法が、世の中を変えるかもしれません。
各種取材や研究に関することなど、
お気軽にお問い合わせください