大学院 工学研究科 情報工学コース 准教授
神戸大学
ネタを作り込んだ漫才やコント等のお笑い鑑賞が楽しく、予約しておいた深夜番組を見るのが至福のひととき。サッカー観戦も好きで、特にひと昔前のイタリアサッカーは選手の戦力の“組み合わせ最適化”を考える上でも興味深いです。
高速で変化するグラフ上での
巡回セールスマン問題に挑む
古くからある数学の難問であり、現在でも盛んに応用問題が研究されている「巡回セールスマン問題(TSP)」。
阿部研究室では、高速に変化するグラフ上でのTSPというさらに難しい問題に対して、その計算時間を最小化するための試みに取り組んでいます。
全ての頂点を一度だけ訪れるツアーを
最小の移動コストで実現するには
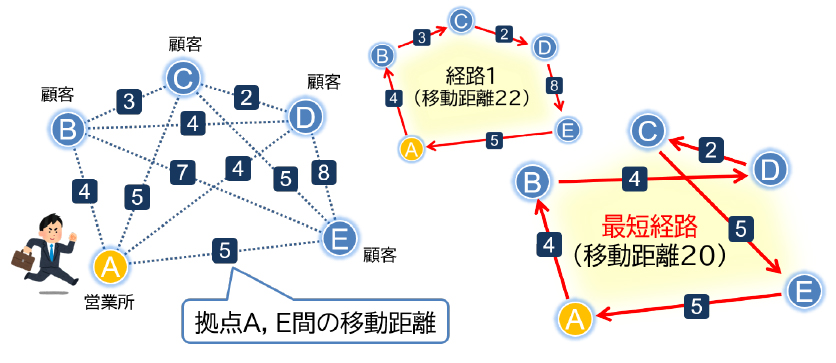
TSPとは、セールスマンがグラフ上の頂点(全ての都市)を一度ずつ巡りながら出発地に戻る際の総移動コストが最小の経路を求める「組み合わせ最適化問題」です。この問題は頂点の数が増えるとスーパーコンピュータを使っても百億年以上かかるほどの計算量を必要とする問題で、数学の世界では「NP困難」と呼ばれるクラスの超難問です。
これは物流やITなどでの効率的なモノや情報の伝達にも活用できます。これまでは変化しない静的グラフを想定して計算していました。しかし、近年では状況が変わりつつあります。例えばSNS上で「バズる」トピックが提供されることがあります。これを更新イベントといいますが、これをきっかけに一気に投稿や閲覧が増加しても、ユーザーSNSを使える状態を維持するには、どのサーバからどのサーバに情報を経由させればいいかを計算しなおす必要があります。時間帯によって経路の混み具合(=辺の重み)が変わると、ツアー(巡回路)も変える必要があります。
阿部研究室では、グラフが表すものが更新イベントによって時間と共に変化するTEGでのTSPを解き、その計算時間を最小化する試みに取り組んでいます。
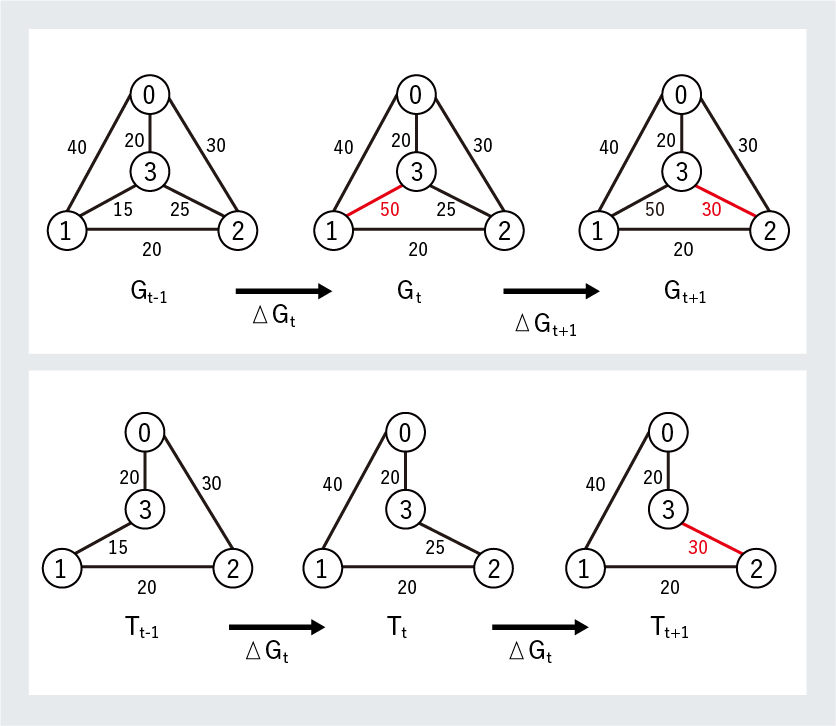
上段)更新イベントによって変化する時間発展グラフ=TEG.
下段)それぞれのグラフごとのTSP最小ツアーとなり,更新イベントによって変化する.
4つのアルゴリズムでTSPを検討し
TEGへの実装・適用が可能であると保証
阿部研究室では、TEG上のTSPを解くためのアルゴリズムを提案。計算時間の短縮のためグラフを並列にたどる分散型アルゴリズムのD-TSP、計算総量の削減のためにグラフの更新イベントの影響を受けるサブグラフの結果のみを再計算するインクリメンタルアルゴリズムのI-TSP、この2つに、それぞれ途中から最短隣接頂点のみを走査する貪欲法と呼ばれるアルゴリズムを組み合わせたDg-TSPとIg-TSPの4つでそれぞれ計算を行いました。
その結果、最も良い解(結果)を出すが、最も遅いのがD-TSPで、逆に最速だが最適な解(結果)とは限らないのがDg-TSPとなり、その間に位置するインクリメンタルアルゴリズムのI-TSPとIg-TSPは、TEGに実装・適用が可能だと保証されました。今後はさらに改良を加えて計算時間の短縮をめざします。
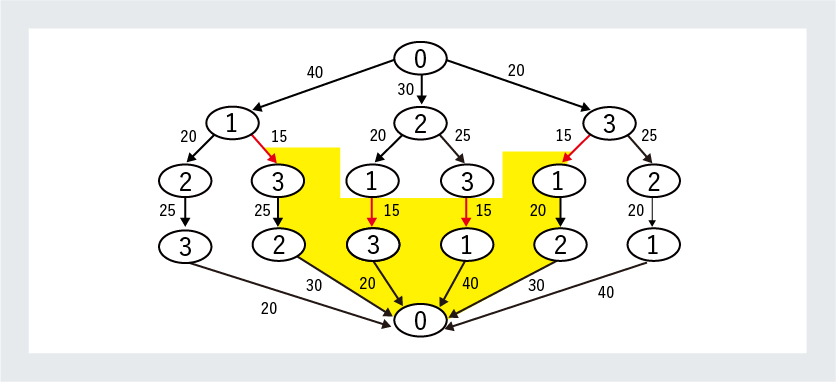
Ig-TSPは,更新イベントが起こった際は黄色い部分を再計算するインクリメンタルアルゴリズムと,最短隣接頂点のみに走査を行う貪欲アルゴリズムを組み合わせたもの.
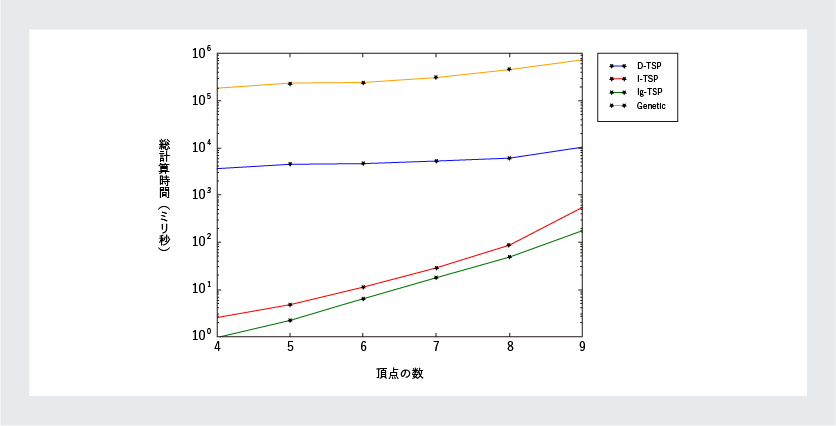
D-TSPに比べ,I-TSPとIg-TSPは計算時間が大きく短縮されている.
巡回セールスマン問題が完全に解決すると
暗号が数秒で解読される!?
巡回セールスマン問題は、たとえば頂点(都市)の数が30になると経路の組み合わせは4.42×10の30乗となり、宇宙誕生から現在までの137億年ですら短く感じるほどの時間がかかります。
ミレニアム懸賞問題にも関わるこの問題を解決するアルゴリズムが作れたら、現在利用されている暗号はすべて一瞬で解かれてしまうでしょう。もちろん、この問題が解かれているなら、現代の暗号に変わる強力なセキュリティ技術が生まれているはずです。
各種取材や研究に関することなど、
お気軽にお問い合わせください