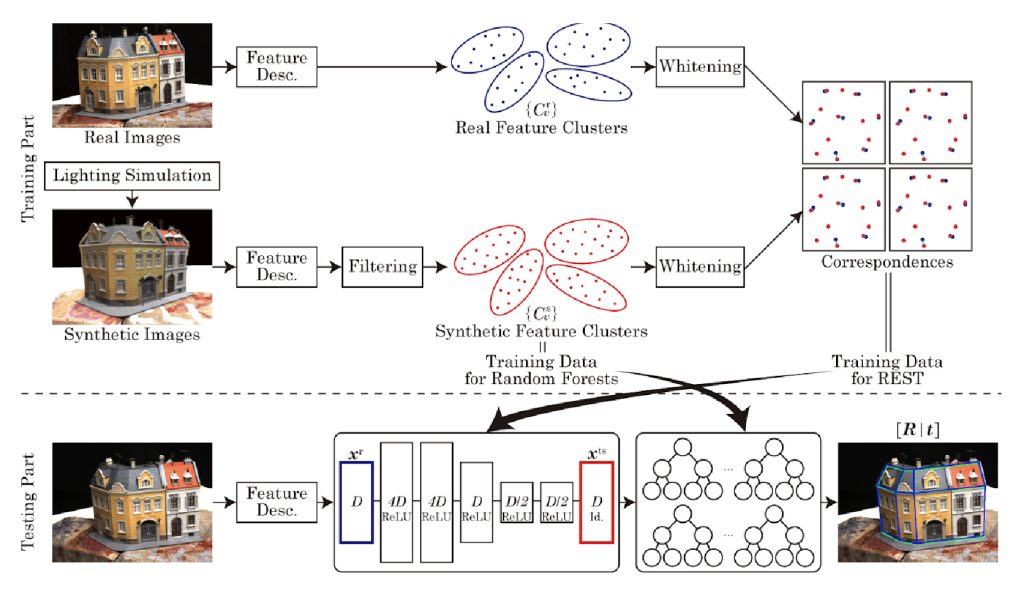
身近にもたくさん存在する最適化問題を解く　
アルゴリズム理論の基礎研究

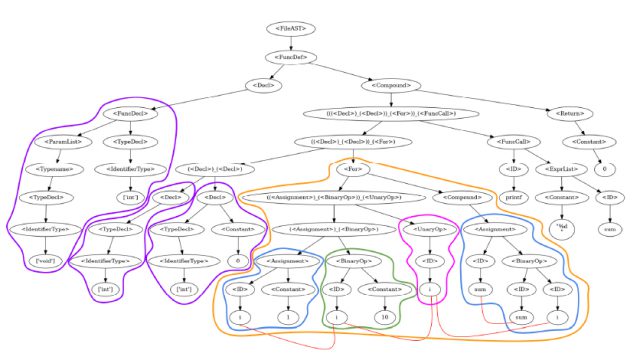
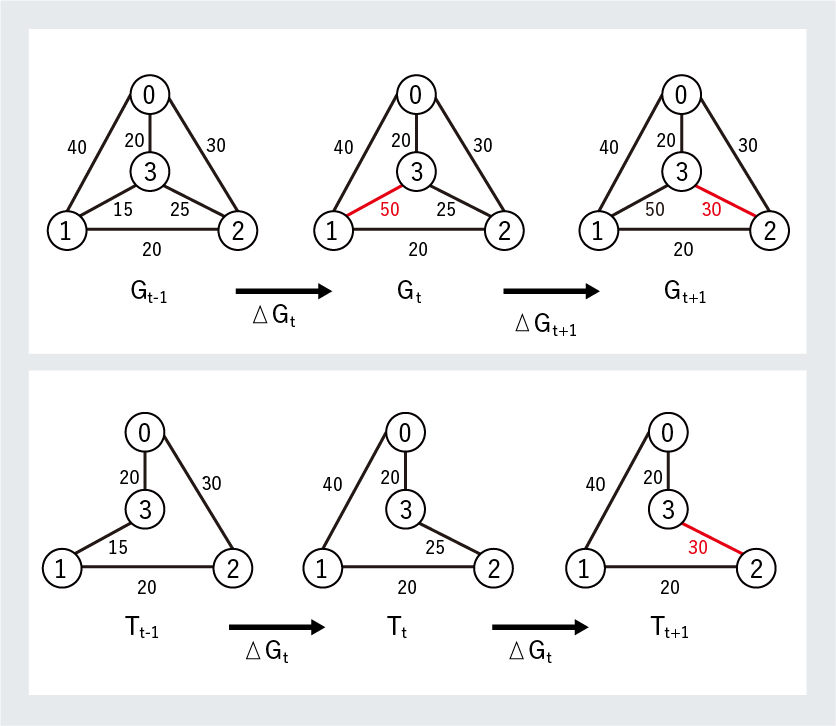
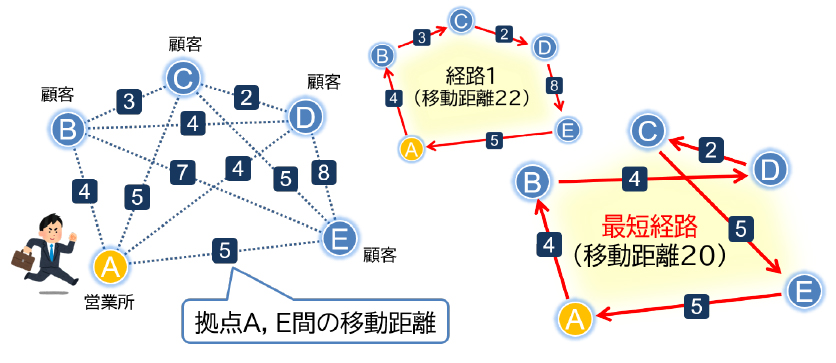
一定の条件を満たす組合せの中から、最もよい組合せを選ぶような問題は、アルバイトのシフト、ルートの検索、スケジューリングなど私たちの身近にもたくさんあります。
上嶋研究室では、こうした「組合せ最適化問題」において効率のよいアルゴリズムのあり方を探っています。

問題が難しいかどうかを証明することが
世の中の問題解決の第一歩になる!?

「組合せ最適化問題」の中には、コンピュータの計算速度が飛躍的に向上しても現実的な時間では解けない問題も存在します。解けない問題ならば、正解でなくても近い答えを得る方法を考えるなど、現実的な対応が取れます。効率の良いアルゴリズムでスパッと解ける問題なら、それを追い求めることになります。

このように、問題が本質的に持っている難しさを明らかにすることは効率の良いアルゴリズム設計の第一歩。問題の本質的難しさを計算困難性と言いますが、上嶋研究室ではその証明とともに、それを活用した暗号技術の基礎研究を行っています。現実的な時間では解けないような難しい問題は、安全性の高い暗号の設計に活用可能なのです。

情報の中身を隠したまま
「情報を知っている」ことだけを相手に納得させる暗号理論

主要な研究テーマの一つは、暗号理論の重要な概念である「ゼロ知識証明」の実現です。

「ゼロ知識証明」とは、パスワードなど秘密情報自体は明かさずに、その情報を知っているという事実を証明するという手法。公開鍵暗号やデジタル署名、ユーザー認証などに応用されている技術です。

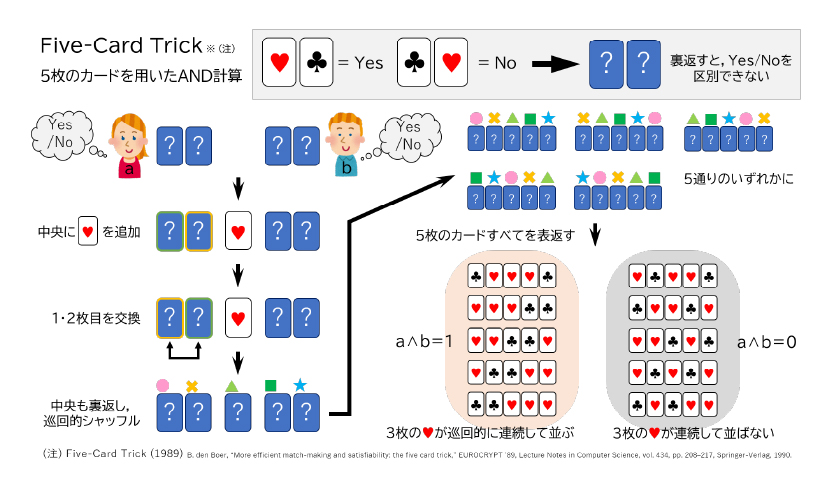
上嶋研究室では、計算困難な問題の中から身近なパズルの問題に着目。「ゼロ知識証明」を実現するプロトコルを、コンピュータではなく、トランプカードのような身近なアイテムを使って設計し、アルゴリズムの最適化を探っています。

暗号機能を手軽に目に見える形で表すこのような設計は、暗号プロトコルについてのデモンストレーションや導入教育に活用できることから最近研究が進んでいる分野です。